Kepler munkássága óta ismert, hogy bármilyen központi égitest körül keringő bolygó és hold pályája ellipszis alakú. De hogy jutott mégis erre a következtetésre a híres csillagász?
A 16. századra az akkor lassan 1400 éves ptolemaioszi geocentrikus világkép már erősen megkopott. A matematikai módszertan és eszköztechnika fejlődése olyan megfigyeléseket tett már ekkor lehetővé, amelyek egyre kevésbé voltak összeegyeztethetők a korábbi elképzelésekkel. Bár ez az évszázadokon átívelő folyamat folytonos volt, a kritikus paradigmaváltás kezdete a lengyel matematikus és csillagász, Nicolaus Copernicus nevéhez fűződik a 16. század első felében. Az 1543-ban nyomtatott, korszakalkotó művében, a De revolutionibus orbium coelestium-ban (Az égi pályák körforgásáról) a geocentrikus modell átfogó, strukturált kritikáját és a heliocentrikus világképének szigorú matematikai megalapozását adta. A közhiedelemmel ellentétben Kopernikusz a heliocentrikus modellt először egy másik, sokkal korábbi, 1514-es művében, a De hypothesibus motuum coelestium a se constitutis commentariolus-ban (Kis kommentár az általa [Copernicus] felállított égi mozgások hipotéziseiről) javasolta.
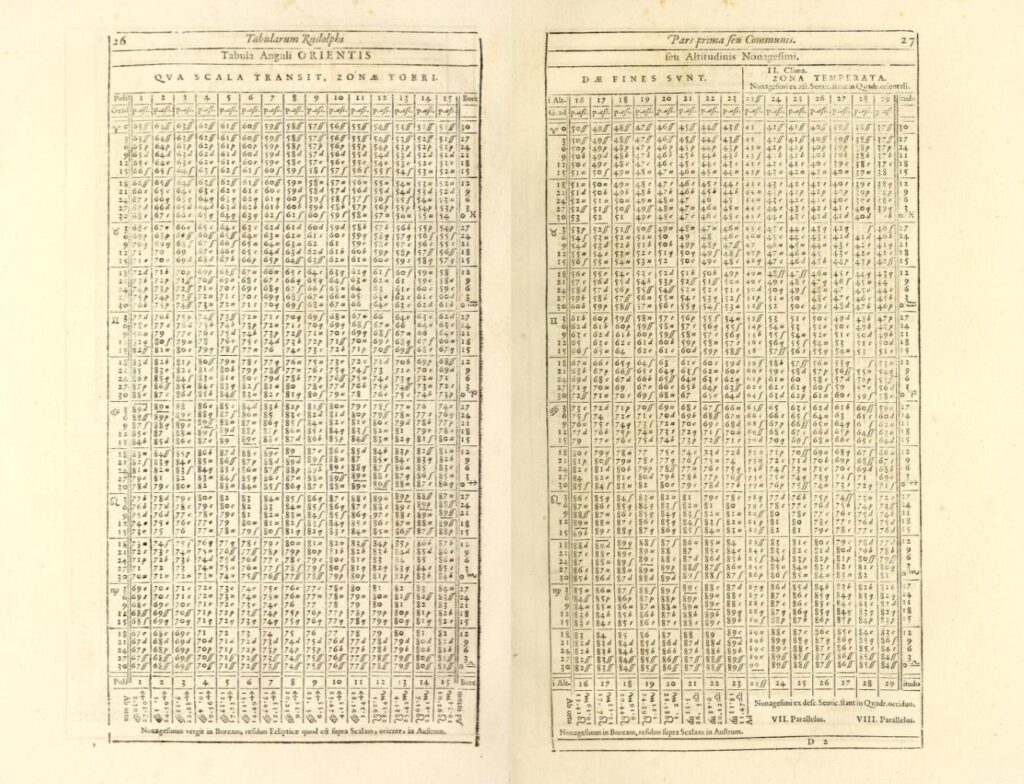
A kopernikuszi modell a ptolemaioszi, komplikált epiciklusok és deferensek nélkül, kvantitatíven magyarázta a bolygók retrográd mozgását, és meghatározta az égitestek relatív elrendezését a Naprendszerben. Azonban ez a modell még mindig a tökéletes körpályák klasszikus feltételezésén alapult, ami már akkor is részben ellentmondásban állt a rendelkezésre álló kevés pontos méréssel. Az alapvető probléma azonban az ilyen megfigyelési adatok és így azok bizonyító erejének rendkívüli hiánya volt. Ebben a bizonytalan időszakban a kor tudósai különféle módosított modellek elképzelésével foglalkoztak – geocentrikusokkal és heliocentrikusokkal egyaránt -, hogy jobban illeszkedjenek a rendelkezésre álló, de kisszámú precíziós megfigyelésre. Végül Tycho Brahe, dán csillagász volt az, akinek a döntő felismerése fölénybe juttatta őt kortársaival szemben. Felismerte, hogy a pontos kép meghatározásához nagy pontosságú pozicionális adatokra van szükség: a bolygómozgások egy soha nem látott méretű és pontosságú katalógusára. Nővérével, Sophia Braheval és egy rendkívül hozzáértő asszisztensekből álló csapattal több mint egy évtizeden keresztül végeztek bolygómegfigyeléseket a dán Hven-szigeten álló Uraniborg obszervatóriumban. Az eredmény egy átfogó pályaadat-katalógus lett, amely később alapot szolgáltatott a Rudolf-táblákhoz, egy csillagkatalógus és bolygótáblázat-gyűjteményhez, amelyet 1627-ben Johannes Kepler, a néhai Brahe egyik asszisztense publikált.
Tycho Brahe 1601-ben bekövetkezett hirtelen halála után Kepler – nem túl lovagias körülmények között – lényegében eltulajdonította az összegyűjtött uraniborgi megfigyeléseket (ami egyébként évtizedekig tartó jogi problémákat okozott neki). Braheval ellentétben Kepler a heliocentrikus modell lelkes támogatója volt, és elszántan igyekezett bizonyítani saját, meglehetősen bonyolult (bár heliocentrikus) elméleteinek helyességét. (Kepler a hat bolygópályát hat egymásba ágyazott gömbként képzelte el, melyek mérete úgy aránylik egymáshoz, hogy közöttük felváltva (képzeletben) pont az öt platóni test helyezkedik el. Ezt az ötletet még jóval felfedezéseinek megjelenése után sem adta fel.) Olyan ötlettel állt elő, amelyet visszatekintve ma akár a tudománytörténet első adattudományi projektjének is tekinthetünk.
Kepler lényegében két releváns adatsorral rendelkezett az Uraniborgban végzett több mint egy évtizedes megfigyelésekből: (i) a bolygók, valamint (ii) a Nap által az égbolton elfoglalt szögtávolságával különböző időpontokban. Sajnos azonban a Föld és a bolygók egyszerre mozognak a pályájukon. Erre a relatív mozgásra vonatkozó mérések egész egyszerűen alulhatározottá teszik az egyenletet a tényleges pályák meghatározásához. A Napon kívül egy másik fix referenciapontra is szükség lenne, ilyen viszont nincs a heliocentrikus modellben. Kepler ezt a referenciapontot végül magában a Marsban találta meg, amelyet Brahe (és maga Kepler is) az akkori korhoz viszonyítva roppant nagy, 1-2 ívperces pontossággal figyelt meg. A Mars sziderikus periódusának, tehát egy marsi évnek a hosszát – ami körülbelül 687 nap – már a babiloni csillagászok is tökéletes pontossággal ismerték, és Kepler idejében már köztudomásúnak számított. Bár Kepler így valószínűleg tisztában volt ezzel a számadattal, Astronomia Nova (Új Csillagászat, 1609) című művében a Brahe-féle megfigyelések alapján ellenőrizte ennek értékét a Mars 780 naponta bekövetkező oppozícióiból – tehát amikor a Föld épp a Nap és a Mars között van – kiszámítva. Kepler zsenialitása abban a felismerésben rejlett, hogy egyszerűen elég volt minden 687. nap megfigyelését figyelembe vennie az uraniborgi adatsorban, ami alatt a Mars – egy marsi év leteltével – visszatért ugyanabba a pozíciójába az égen, ezzel gyakorlatilag másodlagos fix pontként használva azt. Fő művében, az Astronomia Nova-ban, bemutatta a Mars mozgására vonatkozó eredményeit. A lefixált pozíciójú Marsra vonatkozóan éppen elegendő adatpontot tudott kinyerni – melyek mindegyikét egy marsi év választotta el egymástól -, hogy meghatározza belőlük a Föld tényleges pozícióját és egy (még mindig nem teljesen korrekt) körpályát illesszen annak keringési adataira. Ebből kiindulva ezután megpróbálkozott egy körpályát erőltetni a Mars pályaadataira is, de ekkor egy 8 ívperces eltéréssel szembesült az uraniborgi megfigyelések és a feltételezett körpályák között.

Hosszas munka után felismerve, hogy sem a körpályák, sem a ptolemaioszi epiciklusos pályák nem elegendőek, két új posztulátumot javasolt a bolygómozgásra, amelyek már ellipszis alakú pályákat tartalmaztak. Ahogy Kepler azt az Astronomia Nova eredeti kiadásának 113-114. oldalán írja: „Nam si contemnenda censuissem 8 minuta longitudinis, jam satis correxissem (bisecta scilicet eccentricitate) hypothesin cap. XVI. inventam. Nunc quia contemni non potuerunt, sola igitur haec octo minuta viam praeiverunt ad totam Astronomiam reformandam […].„, mely magyar fordításban annyit tesz: „Ha úgy véltem volna, hogy ezt a 8 ívpercet figyelmen kívül hagyhatjuk, […] megfelelően kijavítottam volna már a hipotézisem. Most azonban, mivel nem lehetett őket figyelmen kívül hagyni, ez a nyolc ívperc egymagában kikövezte az utat a csillagászat teljes megreformálásához […].”)
Egy évtizeddel később eredményeit általánosította a Harmonices Mundi (A Világ Harmóniája, 1619) és az Epitome Astronomiae Copernicanae (A kopernikuszi csillagászat kivonata, 1621) című műveiben, ahol egy újabb összefüggést is megfogalmazott, ezzel a bolygómozgás axiómáinak számát háromra emelve. Ez a három összefüggés – amely ma Kepler bolygómozgási törvényeiként ismert – volt az első *modell*, amely matematikailag is precíz, pontos kinematikai leírást adott a Naprendszerre vonatkozóan. Megjelenésükkel a fizika és a csillagászat óriási lépést tett előre, teljesen maga mögött hagyva a tudomány addigi leíró jellegű megközelítését, és belépve az elméleti, magyarázó jellegű tudomány korszakába. Ezzel egy időben, ahogy Galileo Galilei 1609-ben csillagászati célokra kezdte használni az újonnan feltalált távcsövet, minden készen állt a tudományos felfedezések új korszakára.